This a high level overview of HuggingFace’s Deep RL Course. Labs will be done later in a separate session.

Unit 1. Introduction to Deep Reinforcement Learning

Concept

Reinforcement learning is a framework for solving control tasks by building agents that learn from the environment by interacting with it through trial and error and receiving rewards (positive or negative) as unique feedback.

Framework

Agent/Environment + State/Action/Reward.

RL loop outputs a sequence of state, action, reward, and next state.
RL goal is to maximize the cumulative reward, called expected return.

Reward hypothesis

All goals can be described as the maximization of the expected return (expected cumulative reward).

Markov Property

RL process is called Markov Decision Process(MDP). It implies that our agent needs only the current state to decide what action to take and not the history of all the states and actions they took before.

Observations/States Space

State: Complete description of the state of the word (no hidden information).
Observation: Partial description of the state of the word.

Action Space

Discrete: Finite possible actiions.
Continuous: Infinite possible actions.

Rewards and discounting

$R(\tau) = \sum_{k=0}^{\infty}{\gamma^kr_{t+k+1}}$

R: cumulative reward. Gamma: Discount rate. 0.95-0.99. Higher for value long-term. Lower for value short-term.

Type of tasks

Episodic: Starting point and ending point (a terminal state).
Continuing: Task that continue forever (no terminal state).

Exploration/Exploitation Trade-off

Exploration: Trying random actions in order to find more information about the environment.
Exploitation: Using known information to maximize the reward.

Main Approaches to resolve RL problems

Policy, the function that tells what action to take given the state we are in. It defines the agent’s behavior at a given time.

Policy-Based Methods

Learn a function that inputs state and outputs action.

Learn policy function directly. Teaching the agent to learn which action to take, given the current state.

This function will define a mapping from each state to the best corresponding action. Alternatively, it could define a probability distribution over the set of possible actions at that state.

Deterministic: A policy that a given state will always return the same action. $a = \pi(s)$ .
Stochastic: A probability distribution over actions. $\pi(a|s) = P[A|s]$

Value-Based methods

Learn a function that input state and output expected discount accumulative reward. Learn a value function that maps a state to the expected value of being at that state. Teaching the agent to learn which state is more valuable and then take the action that leads to the more valuable state.

$v_{\pi}(s) = E_{\pi}[\sum_{k=0}^{\infty}{\gamma^kr_{t+k+1}}| S_t = s]$

Traditional vs Deep Reinforcement Learning

Traditional Q learning: Use Q table to find which action to take for each state.
Deep Q learning: Use a NN to approximate Q table.

Unit 2. Introduction to Q-Learning

Policy of value-based methods

Always need a policy to direct the agent taking acitions.

In policy-based training, the optimal policy ( $\pi^*$ ) is found by training the policy directly.
In value-based training, finding an optimal value function ( $Q^*$ or $V^*$ ) leads to having an optimal policy. $\pi^*(s) = arg {max}_a Q^*(s, a)$

In value based method, use Epsilon-Greedy Policy that handles the exploration/exploitation trade-off.

Two types of value functions

The state-value function

For each state, outputs the expected return if the agent starts at that state and then follows the policy forever afterwards (for all future timestamps). $V_{\pi}(s) = E_{\pi}[G_t|S_t = s]$

The action-value function

For each state-action pair, the action-value function outputs the expected return if the agent starts in that state, takes that action, and then follows the policy forever. $Q_{\pi}(s, a) = E_{\pi}[G_t|S_t=s, A_t=a]$

The problem is, to EACH value of a state or a state-action pair, we need to sum all the rewards an agent can get if it starts at that state.

The Bellman Equation: Simplify value estimation

Recursive equation. Similar idea to dynamic programming.

$V_{\pi}(s) = E_{\pi}[R_{t+1} + \gamma * V_{\pi}(S_{t+1})|S_t = s]$

Monte Carlo vs Temporal Difference Learning

Monte Carlo: learning at the end of episode

Requires a complete episode of interaction before updating our value function.
With Monte Carlo, we update the value function from a complete episode, and so we use the actual accurate discounted return of this episode.

$V(S_t) \leftarrow V(S_t) + \alpha[G_t - V(S_t)]$

Temporal Difference Learning: learning at each step

Update at one interaction but estimate $G_t$ by adding $R_{t+1}$ and the discounted value of the next state.
With TD Learning, we update the value function from a step, and we replace $G_t$ , which unknown, with an estimated return called TD target.

$V(S_t) \leftarrow V(S_t) + \alpha[R_{t+1} + \gamma V(S_{t+1}) - V(S_t)]$

Introducing Q Learning

What is Q-Learning

Off-policy.
Value-based method. State-value/action value.
Temporal difference (TD) approach.

Q(Quality)-Learning, algorithm to train Q-function, an action-value function that determines the value of being a particular state and taking a particular action.

$\pi^*(s) = arg \max_a Q^*(s,a)$

Q-Learning algorithm

Initialize Q-table

Initialize for each state-action pair. Most of the time, initialize with values of 0.

Choose an action using the epsilon-greedy strategy

Handles exploration/exploitation trade-off.

With an initial values of $\epsilon = 1.0$ :

With probability $1 - \epsilon$ : We do exploitation (agent selects the action with the highest state-action pair value).
With probability $\epsilon$ : We do exploration (trying random action). With training goes on, progressively reduce the epsilon value since Q-table gets better and better in its estimations.

Perform action 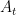$A_t$ , get reward $R_{t+1}$ and next state $S_{t+1}$ .

Update $Q(S_t, A_t)$ .

$Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha[R_{t+1} + \gamma \max_a Q(S_{t+1}, a) - Q(S_t, A_t)]$

$R_{t+1}$ : Immediate reward.
$\gamma \max_a Q(S_{t+1}, a)$ : Discounted estimate optional Q-value of next stage by finding the action that maximizes the current Q-function at the next state.
$R_{t+1} + \gamma \max_a Q(S_{t+1}, a)$ : TD Target.
$R_{t+1} + \gamma \max_a Q(S_{t+1}, a) - Q(S_t, A_t)$ : TD Error.

This is not the epsilon-greedy policy, as the greedy policy, AKA. always take the action with the highest state-action value. Start in a new session and then select action using epsilon-greedy policy again. off-policy.

SARSA

On-policy variant of Q-learning. $Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha[R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t)]$

Off-policy vs On-policy

Off-policy: Using a different policy for acting (inference) and updating (training).
On-policy: Using the same policy for acting and updating.

Unit 3. Deep Q-Learning with Atari Games

From Q-Learning to Deep Q-Learning

Tabular Method: Type of problem in which the state and action are small enough to approximate value functions to be represented as arrays and tables.
Deep Q-Learning: Approximate Q-value with a neural network.

Deep Q-Network

Preparing the input and temporal limitation

Resolves temporal limitations through combining frames.

Deep Q Algorithm

Compares Q-value prediction and Q-target and uses gradient descent to update the weights of our deep Q-Network to approximate our Q-values better.

Q-Target: $R_{t+1} + \gamma \max_a Q(S_{t+1}, a)$
Q-Loss: $R_{t+1} + \gamma \max_a Q(S_{t+1}, a) - Q(S_t, A_t)$

Two phases

Sampling: Perform actions and store the observed experience tuples in a reply memory.
Training: Select a small batch of tuples randomly(??) and learn from this batch using gradient descent update step.

Instability

Combining a non-linear Q-value function (neural network) and bootstrapping (when we update targets with existing estimates and not an actual return).

Solutions:

Experience Replay to make more efficient use of experiences.
Fixed Q-Target to stabilize the training.
Double Deep Learning to handle the problem of the overestimation of Q-values.

Experience Replay

Initialize a replay memory buffer D with capacity N (hyperparameter). We then store experiences in the memory and sample a batch of experiences to feed during training.

Make more efficient use of experiences during training. Reuse during training. Learn from same experiences multiple times.
Avoid forgetting previous experiences (aka catastrophic interference, or catastrophic forgetting).

Random Sampling

Reduce the correlation between experiences. Avoid values from oscillating or diverging catastrophically.

Fixed Q-Target to stabilize the training

Because the use of Bellman equation, we have a TD target and and Q-Value are both calculated based on the same weights, significant correlation between them causing significant oscillation in training.

Use a separate network with fixed parameters for estimating the TD target.
Copy the parameters from our Deep Q-Network every C steps to update the target network.

Double DQN

Double Deep Q-Learning neural networks, handles the problem of the overestimate of Q-values.

Calculating TD target: how to make sure the best action for the next state is the action with the highest Q-value? We don’t have enough information about the best action to take at the beginning.

Use our DQN network to select the best action to take for the next state.
Use our Target network to calculate the target Q value of taking that action at the next state.