Unit 8. Proximal Policy Optimization (PPO)

Introduction

Improves agent’s training stability by avoiding policy updates that are too large by clipping the difference between current and old policy to a specific range $[1 - \epsilon, 1 + \epsilon]$ . Ensure training is stable.

Intuition

Smaller policy updates during training are more likely to converge to an optimal solution.
Too big update can result in falling “off the clip” and takes a long time or even never recover.

Introducing the Clipped Surrogate Objective Function

Recap: The Policy Objective Function (with A2C)

$L^{PG}(\theta) = E_t[log\pi_\theta(a_t|s_t) A_t]$

$log\pi_\theta(a_t|s_t)$ : Log probability of taking that action at that state.
$A_t$ : Advantage function.

Problems:

Too small, training process slow.
Too high, too much variability in training.

PPO’s Clipped Surrogate Objective Function

$L^{CLIP}(\theta) = \hat{E}_t[\min(r_t(\theta)\hat{A}_t, clip(r_t(\theta), 1 - \epsilon, 1 + \epsilon)\hat{A}_t)]$ .

The ratio function

$r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}$ .

If $r_t(\theta) > 1$ , the action $a_t$ at state $s_t$ is more likely in current.
If $r_t(\theta) < 1$ , less likely.

This ratio can replace the probability we use in the policy objective function. AKA, $log\pi_\theta(a_t|s_t)$ .

The unclipped part

$L^{CPI}(\theta) = \hat{E_t}[\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\hat{A_t}] = \hat{E_t}[r_t(\theta)\hat{A_t}]$ .

To clip the ratio so that we limit the divergence of current policy from the older policy.

TRPO(Trut Region Policy Optimization) uses KL divergence constraints outside the objective function. Complicated to implement and takes more computation time.
PPO(Proximal Prolicy Optimization) clips probablility ratio in objective function. Simple.

The clipped objective

$L^{CLIP}(\theta) = \hat{E}_t[min(r_t(\theta)\hat{A}_t, clip(r_t(\theta), 1 - \epsilon, 1 + \epsilon)\hat{A}_t)]$ .

$\epsilon$ is a hyperparameters. In paper it is defined as 0.2.

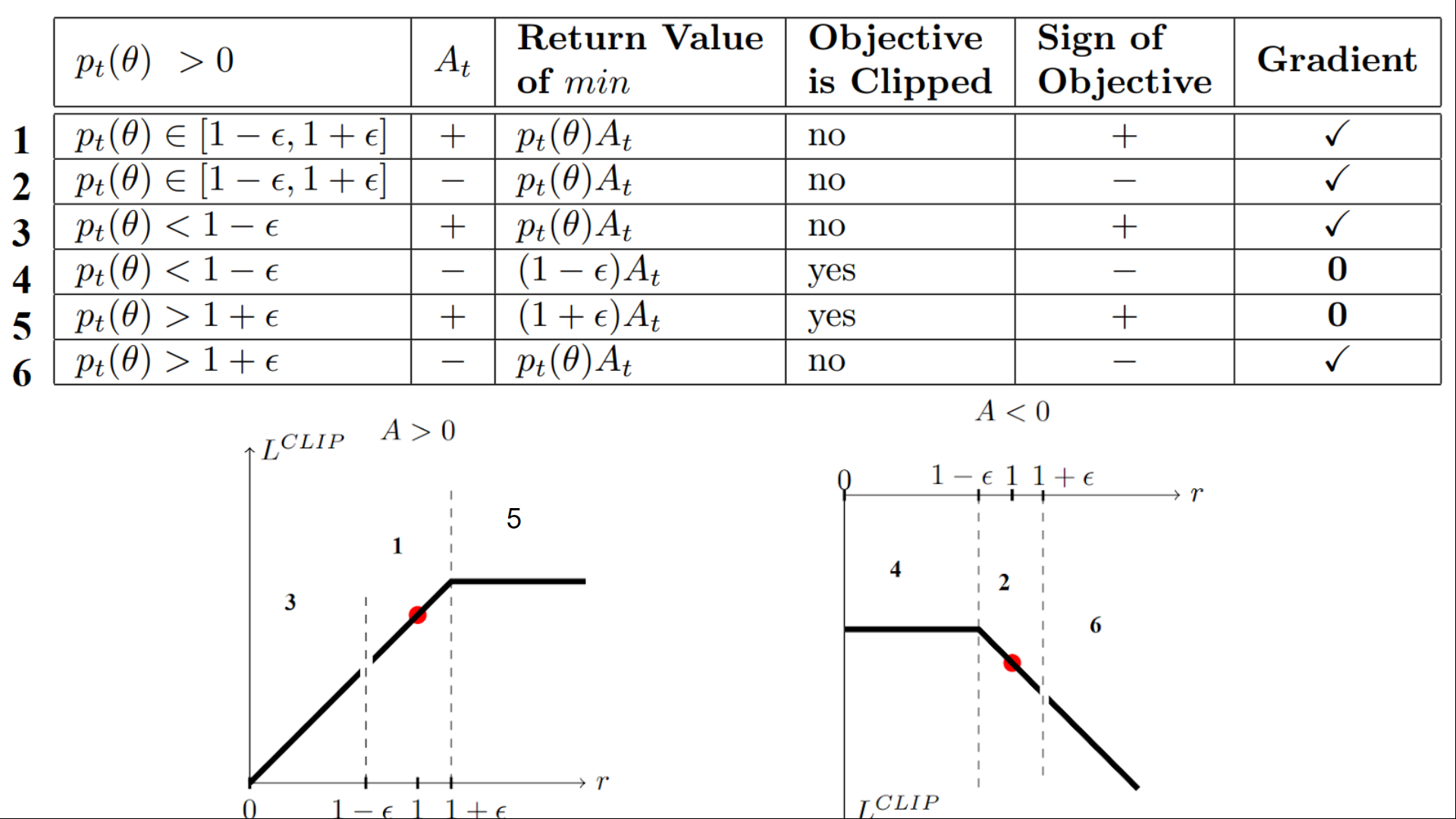
visualize

Unclipped, normal return, normal gradients.
Clipped, clipped return, no gradient, no updates.
- If $r_t(\theta) > 1 + \epsilon$ and $A_t > 0$ , it means we stop aggressively increase a probability of taking the current actition at that state.
- If $r_t(\theta) < 1 - \epsilon$ and $A_t < 0$ , it means we stop aggressively decrease a probability of taking the current actition at that state.

levendlee

Unit 8. Proximal Policy Optimization (PPO)

Unit 8. Proximal Policy Optimization (PPO)

Introduction

Intuition

Introducing the Clipped Surrogate Objective Function

Recap: The Policy Objective Function (with A2C)